
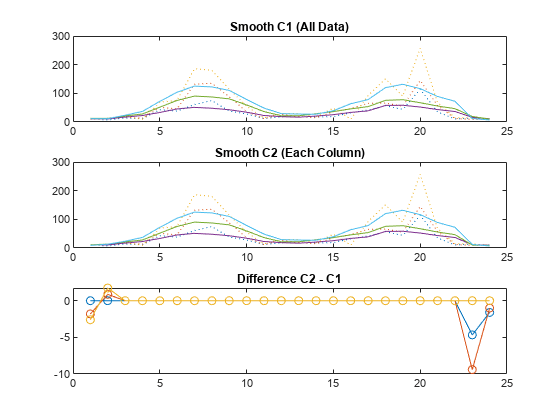
Note that Q ˙ ∗ − Q ˙ l o s s = Q ˙ n e t. T ∗ is the apparent sun's temperature as an exergy source as described in Ref. The entropy generation rate of each component is added as shown in Eq. (6.32) shows the total entropy generation rate in terms of the temperatures and pressures at different locations in the cycle (with reference to Fig. 6.1). The function to be maximized (the objective function), is W ˙ n e t (the net power output). When doing an exergy analysis of the system at steady state and assuming V 1 = V 11 and Z 1 = Z 11 (see Fig. 6.1), the objective function is assembled as shown in Eq. The finite heat transfer and pressure drop in the compressor, turbine, recuperator, receiver, and other tubes are identified as entropy generation mechanisms. (6.32) S ˙ g e n, int = c o m p r e s s o r + d u c t 23 + + Q ˙ l / T ∞ ] r e c u p e r a t o r + d u c t 45 + r e c e i v e r + d u c t 67 + t u r b i n e + d u c t 89 It can be seen from the Colebrook equation, for turbulent flow in smooth pipes the first term within the square brackets is negligible compared to the second term because pipe roughness e is very small. Generally three to four iterations are sufficient to converge on a reasonably good value of the friction factor. This will yield a second approximation for f which can then be used to calculate a better value of f and so on.

We first assume a value of f (such as 0.01) and substitute it in the right hand side of the equation. It is an implicit equation in f because f appears on both sides of the equation.
It can be seen from Eqn (5.101), that to calculate the friction factor f we must use a trial-and-error approach. Therefore, in SI units Equation above is used with e and D expressed in mm. (5.101) 1 / f = − 2 log 10 for R > 4,000īecause R and f are dimensionless, as long as consistent units are used for both e and D, the Colebrook equation is the same regardless of the units employed.


 0 kommentar(er)
0 kommentar(er)
